Année scolaire 2022-2023

---

Lundi 03/07/2023

Petite information : nos deux stagiaires Mme Génier et M. Ba ont brillamment réussi le CAPES externe de mathématiques !

Bravo à eux deux !!

Lundi 19/06/2023

Rédaction du bilan du travail effectué en rapport avec la thèse de M. Auroy, sur les tentatives de mise en place de Dispositifs Préventifls d'Aide, avec l'aide de la co-intervention faite en classe de 3e par Mme Faye et Mme Leconte. Cette rédaction a été incluse dans le bilan de l'action pédagogique portant le même nom (co-intervention entre les deux enseignantes mentionnées).

Ce sera la dernière session du labo de maths pour l'année scolaire 2022-2023.

Lundi 12/06/2023

Suite de l'exposé sur le colloque de la Commission Inter-Irem Didactique de Poitiers, avec le compte rendu des différentes conférences qui s'y sont déroulées, des recherches effectuées et des arguments éventuels "pour" et "contre" énoncés par les conférenciers sur la compétence "modéliser".

Les vidéos de l'évènement :

La conférence d'Alain Kuzniak : https://www.youtube.com/watch?v=hDB_dQJWmDE[/youtube]

La conférence de Berta Barquero et Marianna Bosch (pas de son pendant les deux premières minutes) : https://www.youtube.com/watch?v=KFyVANMnakQ&t=120s[/youtube]

La conférence de Pierre Job : https://www.youtube.com/watch?v=DtYl_TLj0EE[/youtube]

Et la table ronde de cloture (avec ses débats) : https://www.youtube.com/watch?v=utYPUg5lbBA[/youtube]

Lundi 05/06/2023

Retour du colloque organisé par la Commission Inter-Irem Didactique qui s'est déroulé à Poitiers : bilan de la table ronde qui s'est déroulée en fin de colloque, au cours de laquelle les conférenciers présents au colloque (Berta Bergova, Marianna Bosch toute deux venue d'Espagne, et Pierre Job de Belgique), ont échangé avec M. Xavier Sorbe (Inspection Générale de l'Education Nationale), avec pour président de séance Yves Matheron (Professeur des université, Marseille) chargé d'y faire vivre les questions ayant émergées des différents ateliers organisés pendant deux journées intensives de réflexion autour du thème choisi.

Documents : DeuxCyclesColloquePoitiers2023.pdf

Lundi 22/05/2023

Présents : Mme Le Conte, M. Auroy, Mme Génier et Florent

Discussion autour de la compétence "modéliser".

Exposé par M. Auroy d'une présentation, qu'il doit aussi exposer lors du colloque organisé par la Commission Inter-Irem&s Didactique les 25 et 26 mai 2023 à Poitiers, sur le thème de la modélisation. Cette présentation reprend une partie d'un PER sur les fractions, élaboré par le groupe didactique de l'Ires de Marseille, afin d'illustrer le fait que la "modélisation" est un processus ininterrompu d'élaboration de nouveaux savoirs à partir de questions et de limites mis en évidence par des savoirs construits précédemment.

Lundi 27/04/2023

Présents : Mme Le Conte, M. Auroy, Mme Faye (Mme Génier et M. Ba en préparation de CAPES puisque stagiaires M2)

La discussion a porté sur le test réalisée en classe de 3e la semaine précédente, sur le thème des prérequis sur l'entrée dans le chapitre des fonctions.

Le test était organisé en plusieurs exercices :

Les résultats de ce test ont montré les points suivants :

La décision a donc été prise de retravailler le repérage dans le plan au moyen d'exercices progressifs :

Ce système didactique auxiliaire "pré" allait donc se métamorphoser en deuxième système didactique principal, dans lequel le contrat didactique ne contenait pas, au sens du programme officiel de 3e, la dialectique ancien/nouveau, bien que pour la plupart des élèves présents, selon le test, c'était pourtant bien cette dialectique qui était en jeu.

Tous les élèves ayant échoué au test sur ce type d'exercices de repérages allaient être réuni dans le groupe concerné par la séance d'aide qui allait avoir lieu le mercredi 29/03/2023.

Elle a bien eut lieu comme prévue.

Lundi 20/03/2023

Présents : Mme Le Conte, M. Auroy , Mme Genier, M. Ba et Florent
Lecture commune du compte rendu du lundi 13/03/2023 et des remarques faites par M. Auroy à la fin du compte rendu.
Ce dernier a précisé que ses remarques n'étaient que des résumés de ce qui est présent dans le PER sur les relatifs, et que pour plus d'information, il fallait se reporter à ce dernier.

Après cette lecture commune, M. Auroy a présenté l'article écrit par MM. Matheron et Noirfalise en 2002 portant comme titre "L'aide individualisée : entre système didactique auxiliaire inutile et déficit d'analyse didactique entravant son efficacité et son développement". L'objectif n'était pas d'être polémique, mais de présenter le concept de système didactique, avec quelques une de ces caractéristiques, à la fois aux enseignants titulaires du collège, mais aussi et surtout aux stagiaires dont la formation en didactique laisse fortement à désirer, en dehors des concepts pratiques qui leurs sont enseignés comme les types de tâches, les techniques, les technologies, les théories, et les différents moments de l'étude. Cette présentation aura permis de faire découvrir à tous les participants du labo de concepts incontournables qui feront le quotidien des futurs enseignants, comme le contrat didactique, la dialectique ancien/nouveau, et le télescopage de différents systèmes didactiques non (ou mal) étudiés pour vivre ensemble, et comment aider à les faire mieux fonctionner.

Un exemplaire de cet article a été envoyé à chacun des membres présents.

Lundi 13/03/2023

Présents : Mme Le Conte, M. Auroy , Mme Genier, M. Ba et Florent
Le groupe s'est scindé en deux parties :

• Mme Le Conte et M. Auroy afin de discuter d'une intervention (enregistrée et retranscrite) de Mme Le Conte en 3e, à l'occasion d'une expérimentation d'un Dispositif Préventif d'Aide
• Le reste du groupe s'est retrouvé afin d'examiner une question portée par Florent, le jeune stagiaire, portant sur la manière de justifier, en 4e, que le produit de deux nombres négatifs est positif.

Voici, en peu de mots et de manière approximative, ce qui est ressorti du travail du deuxième groupe.

Comment justifier que le produit de deux nombres négatifs est positif ?

1ère solution

Elle consiste à développer une expression comme \(A = -3(-2 + 2)\) :

Tout d'abord, si on suppose la notion d'opposé acquise, la règle de la priorité des calculs entre parenthèses abouti à :

\(A = -3(-2 + 2)\)

\(A = -3 \times 0\)

\(A = 0 \hspace{50pt}\) (1)

D'un autre côté, si on suppose acquise la distributivité de la multiplication sur l'addition et la soustraction, on peut penser à :

\(A = -3(-2 + 2)\)

\(A = -3 \times (-2) + (-3) \times 2\)

\(A = - 3 \times (-2) + (-6) \hspace{50pt}\) (2)

Les résultats (1) et (2) étant égaux, il vient alors que :

\(- 3 \times (-2) + (-6) = 0\)

Deux nombres relatifs opposés ayant leur somme égale à zéro, il vient "naturellement" que \(-3 \times (-2)\) doit être l'opposé de \((-6)\).

2ème solution

On sait que \(2 \times (-3) = -6\). Si P désigne le professeur et E des élèves, on peut alors imaginer le dialogue suivant :

P : Que faut-il ajouter à \(2 \times (-3)\) pour que le résultat soit égal à zéro ?

E : On doit ajouter 6.

P : Que dire de \(2 \times (-3)\) et de \(6\) ?

E : Ils sont opposés.

P : Comment écrire l'opposé de \(2 \times (-3)\) ?

E : \(-2 \times (-3)\)

Bilan de ces deux méthodes

Les deux solutions proposées sont très voisines. Elles font toutes deux appel à des techniques et technologies vue et théoriquement acquises en 5e. Aucune nouveauté théorique dans cette recherche donc, et c'est très bien comme cela car cela permet à un nouveau résultat d'être établi sans avoir recours à des outils théoriques ou technologiques plus lourds. De ce point de vue, tout va bien.

Par contre, dans ces deux techniques, l'utilisation de deux nombres opposés est une donnée dans ce sens que P donne de manière prémédité un calcul dans lequel on trouve deux opposés : le \(2\) et le \(-2\). On peut considérer que c'est là une pratique pédagogique, une sorte d'étayage, sur lequel les élèves vont prendre appui pour prouver ce qui est attendu. La liberté pédagogique étant par définition une liberté du professeur, on ne peut rien redire à cela. Pourtant, on peut se poser la question suivante :

Une partie des élèves pensera peut-être que le résultat sera \(-12\), tandis que d'autres penseront au contraire à \(12\).

Comment prouver qui a raison ?

Des élèves pourraient facilement expliquer, à partir de leurs connaissances des relatifs, que \(-3 \times 4 = -12\) car \(-3 \times 4\) est équivalent à \(4\times (-3) = -3 -3 -3 -3 = -12\)

Il faudrait donc prouver que \(-3 \times (-4)\) est l'opposé de \(-3 \times 4\).

La connaissance de la notion d'opposé amène alors à dire que si \(-3 \times (-4)\) et \(-3 \times 4\) sont opposés alors leur somme est nulle.

Donc il faut calculer \(-3 \times (-4) + (-3) \times 4\).

La subtilité de cette méthode est qu'elle ne présente pas les opposés dès le départ : cela doit venir des élèves ! De même, dans la suite du calcul, ce sont les élèves qui vont devoir penser à la distributivité afin de factoriser l'expression obtenue :

\(-3 \times (-4) + (-3) \times 4 = -3 \times (-4 + 4) = -3 \times 0 = 0\)

La conclusion est immédiate : \(-3 \times (-4)\) et \(-3 \times 4\) sont des opposés. Donc \(-3 \times (-4) = +12 ou 12\)

Cette technique, détaillée dans le PER sur les relatifs créé par le Groupe Didactique de l'Ires de Marseille, présente beaucoup d'avantages sur les deux autres car le questionnement peut, et doit, venir des élèves. C'est d'ailleurs un moyen pour eux de continuer la modélisation de l'ensemble des nombres relatifs entreprise en 5e, à partir des programmes de calculs.

Lundi 06/03/2023

Présents : Mme Le Conte, Mme Faye, M. Auroy , Mme Genier, M. Ba et Florent
Discussion sur les PER existants et les PER qu'il faudrait créer. Un inventaire très sommaire des PER existants a été fait par M. Auroy, conduisant parfois à des demandes d'explication sur leurs contenus respectifs.

Le théorème de Pythagore est un grand absent dans les PER existant. M. Auroy a souligné que ce théorème devrait, selon toute logique épistémologique mais surtout théorique, être amené à partir du théorème de Thalès, lui-même relevant de la théorie des triangles semblables. La recherche du lien entre théorème de Thalès et de Pythagore a donc démarré, avec, auparavant, une recherche de certaines méthodes pour démontrer le théorème de Pythagore (la méthode des aires étant la plus fréquente, avec cependant des approches différentes).

A suivre...

Lundi 27/02/2023

Présents : Mme Le Conte, Mme Faye, M. Auroy , Mme Genier, M. Ba
Discussions sur le prochain test qui sera réalisé en 3e dans le cadre de la mise en place des DPA pilotés par M. Auroy. Le thème du futur chapitre concerné : la notion de fonction (prélude aux fonctions affines et linéaires).

Les thèmes suivant, relevant des prérequis à la notion de fonction, ont été listés :

Lundi 06/02/2023

Présents : Mme Le Conte, Mme Faye, M. Auroy , Mme Genier, M. Ba et Florent

L'heure qui a précédé ce labo

Pendant l'heure qui a précédé la tenue de ce labo, Mme Genier et M. Auroy, accompagnés de M. Ba, on tenter d'étudier les résultats du test que Mme Genier venait de faire passer à ses élèves de 6ème. Ce test portait sur les prérequis jugés nécessaires à l'étude des fractions en 6ème, comme cela a été signalé dans le compte rendu très allégé du lundi 30/01/2023 lisible ci-dessous. Ce tri pris près d'une heure mais à la fin, nous avions une liste d'une dizaine d'élèves pour lesquels nous avons observé des difficultés de nature diverses dans les prérequis. Par exemples :

• le recours aux soustractions répétées pour résoudre un problème de partage en parts égales ;
• le recours à des schémas illustrant des partages ;
• des difficultés pour compter combien de fois une surface unité pouvait être placée dans une autre surface afin de la recouvrir sans chevauchements ni débordements ;
• des difficultés dans certaines opérations, notamment des divisions ;
• une lecture "globale" des nombres écrits en lettres, qui ne permettait pas de prendre en compte l'existence de certains tirets, qui induisait des fautes dans l'écriture de certaines fractions en chiffres (typiquement, la fraction "soixante dix-millièmes" était écrite \(\frac{70}{1000}\) au lieu de \(\frac{60}{10000}\)).

L'heure de labo

Au cours de cette heure, la discussion a porté sur un petit bilan des erreurs rencontrées dans ce test, ainsi que sur le futur chapitre sur les fractions que comptait entamer Mme Génier à la rentrée des vacances d'hiver, soit le lundi 27/02/2023.

Ce chapitre à venir concerne la fraction partage, très souvent présentée sous une forme maladroite avec une figure découpée en plusieurs parties égales dont certaines coloriées, et, placée en regard de cette figure, une fraction généralement expliquée, en primaire mais aussi en 6ème, comme étant "le nombre de parts colorées" sur "le nombre total de parts".

Pour plus de détails sur ce qui a déjà été expliqué sur le thème des fractions dans ce labo de maths, on peut se référer aux sections suivantes : lundi 21/11/22, Lundi 19/09/22

Lundi 30/01/2023

Présents : Mme Le Conte, Mme Faye, M. Auroy , Mme Genier, M. Ba et Florent (stagiaire en L2 Informatique venu assister à des cours de sa tutrice).
Après la présentation de Florent, le groupe s'est attelé à l'examen du test des prérequis, prévu dans la classe de 6e confiée à Mme Génier, sur le thème des fractions. Ce test était prévu pour le jeudi 2 février. Quelques modifications ont été faites sur le projet échangé par mail entre Mme Genier et M. Auroy.
Le reste du temps a consisté à en savoir un peu plus sur notre invité du jour, ses études, son projet, ainsi que sur ce qui pouvait se faire au sein de ce labo de maths (pourquoi il avait été créé, son ou ses objectifs, etc.). Nous espérons que Florent reviendra quand il le pourra et qu'il a passé un bon moment en notre compagnie, tout comme nous avons été enchanté de sa présence.

Lundi 23/01/2023

Présents : Mme Le Conte, Mme Faye, M. Auroy , Mme Genier, M. Ba.
La discussion a porté sur un thème récurent chez les enseignants de mathématiques : Comment aborder l'algèbre au collège ?

A toutes les questions qui peuvent se poser sur ce sujet, un PER sur l'algèbre au collège, réalisé par le Groupe Didactique de l'IRES de Marseille, est en train d'essayer d'y répondre. Bien qu'inachevé, en voici son déroulement global :

I - D'abord, les nombres relatifs

L'entrée par les nombres relatifs est impératifs, à condition d'être fidèle à ce qui va suivre : les nombres relatifs vont être introduits à partir de programmes de calculs ! .

Pourquoi cela ?

Tout simplement parce que ces nombres relatifs ne peuvent pas être des mesures de grandeurs, et qu'il est dès lors impossible de déterminer des situations concrètes pour les aborder. Les enseignants qui usent et abusent des températures, des histoires de gains et de pertes et autres types d'activités comme des niveaux de sous-sols et autres joyeusetés doivent comprendre que ces "situations concrètes" ne respectent pas la définition d'une mesure pour les deux raisons suivantes :

Ces deux caractéristiques ne sont clairement pas vérifiées dans toutes les situations "concrètes" énoncées plus haut. Il faut les abandonner !

Il restait deux entrées possible :

II - Ensuite des activités pour motiver l'utilisation de lettres dans les programmes de calculs

Il s'agit d'activité bien connues de carrés bordés ou de maison en allumettes.

Bien amenées, ces activités permettent aisément de montrer tout l'intérêt des lettres dans les programmes de calculs.

Car les élèves doivent éprouver le besoin de simplifier les programmes de calculs qu'ils obtiennent dans ces activités !

III - Puis les comparaisons de programmes de calculs

Il faut amener les élèves à obtenir plusieurs programmes de calculs pour le même problème et se servir de ces programmes de calculs pour vérifier d'abord qu'ils sont bien équivalents.

Des tests numériques auront lieu.

Ensuite, quand ils auront rencontré beaucoup de programmes de calculs équivalent dans beaucoup de situations, la question viendra : Nous avons vu que les programmes de calculs étaient équivalents. Mais pourquoi le sont-ils ?

Ce sera le moment de rencontrer la nécessité de travailler ces programmes de calculs avec des outils comme la factorisation, le développement, la présence d'un signe " \(-\) " devant des parenthèses, des simplifications, etc. Les programmes de calculs étudiés par l'algèbre, cette dernière étant vécue comme une nécessité !

IV - Enfin, les équations

Et enfin viendront les équations, c'est à dire les programmes de calculs qu'il faut reprendre à l'envers afin de remonter à la grandeur inconnue.

Lundi 16/01/2023

Présents : Mme Le Conte, Mme Faye, M. Auroy .
Retours sur la séance de DPA anté où les élèves ayant peu ou pas répondu au test d'entrée du chapitre ont pu bénéficier d'une heure pour se remémorer différentes techniques relatives aux situations de proportionnalité. Six élèves avaient été retenus pour cette séance de DPA, mais seulement trois étaient présents. La transcription de la séance montre plusieurs points importants, à savoir :

1. Les élèves concernés ne lisent pas correctement les énoncés, et surtout, ne font pas assez attention aux unités présentes : la volonté visible de "faire plaisir au professeur" les pousse alors à proposer des additions avec des nombres aux unités différentes, ou à répondre à des questions qui ne sont pas posées ;
2. Le passage à l'écrit, lors du moment exploratoire pour commencer à chercher un exercice, ne constitue pas un automatisme : pour eux, il semble que le passage à l'écrit ne doit se faire que lorsqu'ils ont "pensé" à une solution. Le reste se fait "mentalement", comme s'ils pouvaient tout gérer de tête ;
3. Ce moment exploratoire est rarement le moment d'un questionnement clair de la part des élèves : les nombres semblent dissociés des grandeurs qu'ils mesurent. A cela s'ajoute des problèmes de vocabulaire qui font obstacle à la compréhension des situations évoquées dans les problèmes. La part du professeur devient alors plus importante que prévue, car les élèves ont besoin d'explications, ce qui entraine des aller-retours très fréquents entre consignes et explications, d'où une concentration peu soutenue ;
4. Les élèves faibles semblent "prisonniers" d'apprentissages et d'analogies naïves qui les bloquent dans leurs réflexions : par exemple, le mot "agrandir" n'est associé qu'à l'opération "addition". De fait, la présence du mot "agrandir" devient un obstacle plutôt qu'une aide à la compréhension de la situation décrite. Il en est de même pour le mot "réduction" qui, lui, est associé à la "soustraction" au lieu de la "division" ;
5. Les rapports entre les sous unités sont non maîtrisés : si le \(mm\) est reconnu comme étant plus petit que le \(cm\), les élèves présents montrent que, pour eux, diviser des \(cm\) par un scalaire donne de facto des \(mm\). La signification des préfixes leur est complètement inconnue ;
6. Certains " ostensifs " jouent néanmoins leur rôle : à la vu d'un tableau de proportionnalité, la règle des produits en croix est vite reconnue par l'un des élèves (quand bien même l'élève en question n'était pas capable de résoudre un problème de proportionnalité simple en début de séance). La présence de ce tableau agit bien comme tout ostensif normalement intégré par un élève : la technique surgit tout de suite. Il y a donc bien, dans les acquis de cet élève, un lien entre tableau de proportionnalité et produits en croix, mais percevoir la proportionnalité dans un énoncé écrit en langage naturel lui est impossible ;
7. De fait, quand le professeur demande aux élèves d'expliquer en quoi consiste une situation de proportionnalité, aucun d'eux n'est en capacité de répondre. Ce terme n'a pour eux aucun sens.

Lundi 09/01/2023

Présents : Mme Le Conte, Mme Faye, M. Auroy .
La discussion a porté sur le type de remédiation apporter aux élèves de 3e2 ayant commis beaucoup d'erreurs dans le test donné la semaine précédente sur le thème de la proportionnalité. Il a fallu choisir quel type d'exercices ou d'activités proposer aux élèves concernés, quoi dire ou éviter de dire, quels éléments de langage devaient venir d'eux, etc. Nous avons opté pour des exercices où :

Il a aussi fallu décider quels types d'exercices proposer au reste de la classe. Nous avons opté pour des exercices classiques sur la proportionnalité où les enjeux étaient :

En effet, lors de la correction du test, nous avons remarqué que beaucoup d'élèves ne possédaient souvent qu'une seule technique, et que celle-ci était rarement la méthode la plus "puissante" (l'utilisation de l'égalité des produits en croix, dans un tableau de proportionnalité ou dans des suites de fractions égales).

Lundi 12/12/22

Présents : Mme Génier, M. Ba , M. Lemasson, Mme Le Conte, M. Auroy .

1 - La question du jour

La discussion a démarré à propos d'une question de M. Lemasson sur la décomposition d'un nombre décimal en somme de fractions décimales, comme celle-ci :

et de son lien avec une décomposition décimale, comme celle-là :

C'est à dire, en d'autres termes, sur la nature de l'association suivante :

Très (trop) souvent, cette association est "donnée" aux élèves, et non motivée mathématiquement.

La question a donc été la suivante :

Cette question, pour "banale" qu'elle soit, mérite qu'on s'y attarde car elle rend compte d'une part de l'incohérence des programmes officiels sur le sujet tout autant que des difficultés que rencontrent les enseignants pour répondre aux injonctions de l'institution.

2 - Les difficultés rencontrées par les enseignants

Les repères annuels de progression du cycle 3, notamment celui de 2016, prévoient que les élèves de CM1 apprennent à utiliser les nombres entiers jusqu'au million, sans préciser du temps qui sera nécessaire à cet apprentissage. Ensuite, sur la Période 1 (qui correspond à un cinquième du temps scolaire, hors vacances) ils doivent apprendre à utiliser les fractions de grandeurs. En période 2, ils doivent apprendre les fractions décimales de grandeurs, ainsi que leurs équivalences avec les nombres décimaux, comme l'a montré notre question du jour exposée plus haut.

On pourrait donc croire l'affaire classée depuis le CM1.

Mais si l'on se réfère à l'analyse du problème des fractions de grandeurs exposée ci-dessous, correspondant au labo du lundi 21/11/22, il est clair que l'enseignement des fractions est problématique.

On objectera peut-être qu'il là s'agit d'un exemple isolé, et qu'à l'instar d'une hirondelle qui ne fait pas le printemps, un exercice mal pensé ne représente pas l'ensemble de ce qui se fait dans les écoles primaires sur les fractions.

Cela étant dit, n'importe quel enseignant de mathématiques en 6è pourra témoigner que ni les nombres entiers, ni les fractions, ni les nombres décimaux ne sont acquis par les élèves arrivés en 6è, quand bien même ils les utilisent depuis le CM1, voir avant.

C'est que le problème est sans doute bien plus ardu que les "simplistes" injonctions de l'institution ne pourraient le laisser croire.

3 - Quel est le problème avec tous ces nombres ?

En effet, l'apprentissage des nombres entiers, des fractions, des nombres décimaux, etc. correspond à une logique historique, dépendant des progrès techniques et scientifiques tout autant que des besoins des sociétés dans lesquels leur nécessité a fait loi : les nombres entiers ne permettent pas de décrire ce qui se passe entre deux entiers, d'où la création des fractions. Les fractions ne permettent pas d'écrire tous les nombres existant entre deux entiers, ni d'effectuer des calculs facilement, correspondant à la nécessité d'effectuer des mesures de plus en plus précises de certaines grandeurs, d'où les nombres décimaux.

A chaque nouvel ensemble de nombre correspondent des avancées par rapport aux précédents, mais aussi de nouvelles limites.

Leur "donner" des correspondances entre différents "ostensifs" (signes/symboles visibles permettant d'écrire les nombres entiers, les fractions rationnelles, les fractions décimales, les nombres décimaux ou non, etc.) ce n'est pas leur "enseigner les mathématiques", c'est les empêcher de les apprendre tout en leur faisant croire qu'ils les ont bien appris.

Réaliser cet apprentissage convenablement nécessite de suivre un véritable "parcours" dans lequel les rencontres des raisons d'être et des limites seront vécues, éprouvées, dépassées.
Ce parcours doit s'intégrer au temps institutionnellement établi pour ce faire, mais il est possible que ce dernier soit trop court pour le permettre, sans compter les insuffisances dans la formation professionnelle des enseignants en mathématiques (professeurs des écoles et des collèges) chez qui les compétences en didactique reculent depuis quelques années, ce qui ne veut pas dire qu'elles étaient suffisantes à leur plus haut niveau.

A ce jour, le groupe didactique de l'Irem-Ires de Marseille est le seul à s''être attelé à ce "parcours", depuis maintenant près de 3 ans, pour le mettre au point et le tester en classe, face aux élèves. Ce travail reste à terminer.

Autres questions abordées lors de cette session du labo

Les questions précédentes ont débouché naturellement sur les "ostensifs" utilisés en mathématiques, notamment les symboles des quatre opérations, l'écriture fractionnaire, etc.

Il se trouve qu'un site web propose un petit inventaire de quelques symboles, ainsi que leurs dates d'apparitions et les noms de leurs inventeurs. Cette page est consultable ici.

Notons que les règles de priorités des opérations, enseignées en 5è, si elles sont bien pratiques, n'empêchent pas quelques problèmes, qui pourraient apporter des débats intéressants en classe.
Par exemple, quel est le résultat de :

La présence de l'obèle "\(\div\)" suivi d'une multiplication dont l'un des facteurs est entre parenthèses fait intervenir deux sortes de priorités : celle de la multiplication et de la division, et celle des calculs entre parenthèses. Mais laquelle de ces priorités est elle-même "prioritaire" sur l'autre ?

Pour avoir un petit aperçu tant historique que mathématique de la question, on peut utilement aller visionner la vidéo de Mickaël Launay sur le sujet en se rendant sur ce lien : https://www.youtube.com/watch?v=tYf3CpbqAVo .

Lundi 28/11/22 et Lundi 05/12/22

Pas de labo pour cause d'absence de M. Auroy.

Lundi 21/11/22

Présents : Mme Génier, M. Ba , M. Lemasson (remplaçant Mme Faye), M. Auroy .

Au hasard d'une navigation sur Internet, M. Auroy a vu circuler l'exercice suivant :

Présentation du problème

M. Auroy a distribué une image de ce problème aux membres du labo en leur demandant de l'étudier et d'en dégager les points positifs et négatifs. Voici les éléments signalés :

Points positifs

Points négatifs

Analyse commune de cet exercice

A propos de l'unité \(u\)

Cet exercice donne donc à voir une “bande”, affublée d’un \(u\) qui semble nommer une “unité”. Cette bande serait donc un “objet”, nommé \(u\), non mesurable en tant que tel. Seulement, un problème survient alors : on ne peut pas mesurer un objet, on ne peut que mesurer les grandeurs qui se rattachent à cet objet.

Par conséquent, si \(u\) désigne l'objet "bande", toute fraction de cet objet n'a aucun sens mathématique (certes, la "part de pizza" est, par abus de langage, une fraction d'un objet, mais n'importe qui sait qu'il s'agit en réalité de la surface totale de ladite pizza qui est découpée, et non l'objet "pizza").

Les grandeurs ici présentes sont :

• une longueur, mise en évidence par une ligne noire épaisse,
• une surface, mise en évidence par un quadrillage régulier.

On se doute que le mot “longueur”, présent dans la consigne de l'exercice, parle en réalité de la mesure du plus grand côté du rectangle tracé en noir épais. Seulement, c’est la ligne noire épaisse qui est mise en évidence, pas le plus grand côté du rectangle tracé en noir. Et il n’est écrit nulle part, ni même pas sous-entendu dans cet exercice, que \(u\) désigne la mesure du grand côté du rectangle. Au contraire, on a bien l’impression que ce \(u\) désigne l’objet “bande” en entier, voir, au mieux, sa surface, vu que la lettre est à l’intérieure de l’objet.

Par conséquent, la consigne qui parle de "longueur" est incompréhensible.

A propos des réponses proposées

Ainsi, si l’on observe les propositions de réponses parmi lesquelles il fallait choisir la bonne pour chaque question, il se trouve qu’aucune ne convient :

• \(\frac{1}{2}u\) n’a aucun sens car \(u\) n’est pas indiquée explicitement comme étant la mesure du plus grand côté du rectangle noir ; même constat pour \(\frac{1}{4}u\) ou \(\frac{1}{3}u\)
• \(1 + \frac{3}{6}u\) est absurde car d’une part \(\frac{3}{6}u\) n’a pas de sens, mais en plus la somme \(1 + \frac{3}{6}u\) est impossible à calculer puisque le \(1\) n’a pas d’unité ; même constat pour \(1 + \frac{1}{3}u\).

Par ailleurs, un élève a de quoi être dérouté : les propositions A, B et C montrent uniquement des surfaces. La ligne noire a disparu. Il semble donc que ces trois cas parlent de surfaces, et non de longueur.

Bilan de cet exercice

Cet exercice fait soupçonner plusieurs choses impossible à vérifier par manque d'information sur ce qui a été travaillé réellement en classe. Cependant, on peut constater les points suivants :

1. La confusion entre un objet et les grandeurs qui lui sont associées semble profonde chez l’enseignant, et donc chez les élèves. C’est hélas un problème très répandu chez les enseignants, qu’ils soient en primaire ou en collège.
2. Le mot “longueur” semble implicitement lié au plus grand côté d’un rectangle, ce qui ici pose un problème car la ligne noire, qui est aussi une longueur, est visuellement très prégnante et fait, d’une certaine manière, obstacle à la prise en compte de la longueur (implicite) du rectangle noir. Elle représente un périmètre, et pas la longueur (implicite) du grand côté du rectangle noir.
3. La disparition de la ligne noire dans les trois cas A, B et C incite à prenser à des surfaces. Cette disparition entre donc en contraction avec d'une part le fait d’avoir rendue visible la ligne noire au départ, et d'autre part avec la consigne qui fait intervenir la notion de "longueur".
4. Les trois cas A, B et C sont étiquetés Bande A : …….., Bande B : …………. et Bande C : ………….. alors qu’il aurait fallu écrire : longueur de la bande A = ……………….., longueur de la bande B = …………….. etc. à condition d’avoir appelée \(u\) la longueur de la bande unité donnée au départ, ce qui n’a pas été fait.
5. Au final, on ne peut que compatir avec l’élève qui a fait faux, car ce n’est pas lui le problème, ni le fait que l’enseignement sur les fraction soit acquis, ou en cours d’acquisition on non acquis. Cet exercice est une aberration mathématique, un bel exemple à montrer en formation pour informer les futurs professeurs (de collège ou de primaire) sur la nécessité de parler des grandeurs avant de parler de mesures, et de parler de fractions de grandeurs au lieu de fractions d’objets.

Ce qu'aurait dû être cet exercice

Voici, à notre avis, comment cet exercice aurait dû être présenté lors de l’évaluation, ou lors des exercices qui ont précédés cette évaluation :

Dans cet exercice, \(u\) désigne la mesure du segment tracé ci-dessous :

Réponses possibles :

Dans chacun des cas suivant, indiquez la mesure de la longueur du segment tracé en choissant votre réponse parmi celles qui sont proposées ci-dessus.

Cas A : 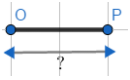--> Mesure du segment : ………………………………………

etc.

Lundi 14/11/22

Présents : Mme Le Conte, Mme Génier, M. Ba , M. Auroy .

Invités spéciaux : M. Ricomet (IA-IPR des Bouches du Rhône) et Bénédicte ESPARIAT (Chargée de Mission académique pour le déploiement du plan Mathématiques)

L'Inspection Académique ayant été mise au courant de l'existence du labo de maths du collège Longchamp, une rencontre avec ses délégués chargés de recenser les labos de maths de l'Académie devait se produire. Ce fut aujourd'hui le grand jour.

Les discussions ont porté sur les raisons d'être de ce laboratoire (au départ, uniquement de réaliser un espace de discussion entre collègues, notamment sur les contenus des cours) et sur ses activités (discussions didactiques sur les contenus des cours et les savoirs à transmettre, ainsi que leurs raisons d'être, puis, au fil des années, la contribution à la formation pratique des stagiaires, puis à la lecture commune et l'utilisation des PER mis au point par divers instances, notamment par l'Irem de Marseille, au travers de travaux du groupe didactique dirigé par M. Yves Matheron, Professeur des Universités, et dernièrement enfin la mise en place de dispositifs préventifs d'aide dans le cadre de la thèse menée par M. Auroy).

La liaison école-collège a aussi été évoquée, ainsi qu'un projet de journée de formation et conférence(s) sur des thèmes mathématiques susceptibles d'intéresser les professeurs des écoles situées aux alentours du collège Longchamp, ainsi les professeurs des collèges (par exemple sur la notion de fraction). A suivre...

Lundi 07/11/22

Présents : Mme Le Conte, Mme Faye, Mme Génier, M. Ba , M. Auroy .
Reprise de nos activités.

A venir : Préparation du contenu du prochain test en 3e sur la proportionnalité comme, ainsi que sur la remédiation éventuelle sur ce thème afin d'aborder le théorème de Thalès avec des techniques éprouvées. Cette remédiation devra permettre aux élèves de retrouver les techniques associées au thème de la proportionnalité dans diverses situations, sans que le professeur ne donne de réponses : par interaction avec les exercices proposés, il faudra que les élèves parviennent à se corriger jusqu'à obtenir les résultats espérés par des techniques fiables, explicites, le professeur validant ces savoirs (re)découverts et mis au point.

Lundi 17/10/22

Présents : Mme Le Conte, Mme Faye, Mme Génier, M. Ba (stagiaire nouvellement arrivé), M. Auroy .
Réflexions sur un test d'entrée portant sur les bases de la géométrie euclidienne.
Mise au point d'une progression en géométrie (trois séquences durant environ 3 semaines) :

Lundi 10/10/22

Présents : Mme Le Conte, Mme Génier, M. Auroy - Mme Faye était en sortie culturelle avec les classes de 3e.
Etude des modifications apportées par Mme Le Conte au test prévu pour ses classes de 4e sur les pré-requis permettant de de suivre et comprendre la séquence à venir sur les puissances de 10 et leur utilisation dans le calcul scientifique.

Lundi 03/10/22

Présents : Mme Le Conte, Mme Faye, Mme Génier, M. Auroy .
Mise au point du prochain test qui sera réalisé en 3e dans le cadre de l'expérimentation des Dispositifs Préventifs d'Aide.
Le prochain chapitre concernera le calcul littéral, il a donc été convenu de tester les prérequis suivants :

Lundi 26/09/22

Suite de l'analyse du PER sur les fractions afin de déterminer à quel moment on doit s'arrêter relativement au programme de 6e.

Lundi 19/09/22

Le PER sur les fractions

Historiquement, l'étude des fraction remonte à une période très lointaine (3000 an av. JC environ). Les fractions étaient utilisées pour des calculs liés à l'astronomie, avec des dénominateurs multiples de \(60\). Il s'agissait donc de mesures liées à des observations. Ces observations reposent sur les objets qu'on voit, qu'on peut éventuellement toucher, qu'on peut additionner ou soustraire, et qu'on peut comparer. En mathématiques, on appelle ça des grandeurs mesurables et calculables, ce qui fait des mathématiques, à l'origine, la science de l'étude des grandeurs.

Ce qui se cache derrière les fractions c'est donc des mesures de grandeurs grâce à des grandeurs de même espèce, plus grandes ou plus petites. C'est de la théorie de la mesure et de la fabrication d'unités de mesures dont il s'agit en réalité (les différentes expériences présentent dans le PER amènent ce constat sur lequel il faudra insister) : les fractions doivent apparaitre à un moment comme des nombres mesurant une grandeur par rapport à une autre grandeur de même espèce ! . C'est tout l'enjeu du départ du PER sur les fractions.

Préambule à propos des grandeurs (à faire en classe)

Concrètement, pour faire vivre ces différentes règles en classe, il faut amener les élèves à chercher toutes les différences que plusieurs objets possèdent les uns avec les autres, et montrer que, parmi ces différences, certaines sont de natures à obéir aux trois règles ci-dessus, tandis que d'autres non. Par exemple, apporter trois livres très différents en "tailles" (surface, largeur, hauteur, épaisseur et donc volume et masse) et demander aux élèves : quelles sont les différences entre ces trois livres.

Là, les réponses vont fuser : couleurs, titres, auteurs, maisons d'éditions, dates de parution, etc. hauteur, surface, nombre de pages, nombre de mots, de phrases, épaisseur, masse. Le truc est qu'à l'énoncé, par les élèves, de toutes ces différences, celles-ci sont écrites sur le tableau sur deux colonnes (sans le dire) : celles qui sont mesurables et calculables, et les autres. C'est l'affaire d'une heure environ. Ainsi, on va pouvoir leur montrer que :

• les numéros de pages ne peuvent pas s'additionner ("additionner la page 3 à la page 7 ne donne pas le contenu de la page 10), alors que les nombres de pages peuvent s'additionner, se soustraire, se comparer, se classer par ordre croissant ou décroissant, etc.
• Même chose pour les largeurs des livres, des hauteurs, des épaisseurs, des surfaces (pour les volumes, c'est infaisable avec des livres bien sûr), les masses (en faisant soupeser les livres mis les uns sur les autres on obtient une masse plus lourde, etc.
• et insister sur le fait que les grandeurs non calculables ne seront jamais étudiées comme tel, bien que des questions pourront apparaitre les concernant (style : combien d'année se sont écoulées entre 2022 et 1965 ?)

L'idée est de leur faire prendre conscience que des grandeurs peuvent s'additionner, se soustraire, se comparer, et d'autres non, bien qu'elles soient exprimées avec des nombres. On peut aussi leur parler des températures, ou des dates (additionner l'année 2022 avec l'année 2023 ne nous dira pas ce qu'il y aura au cours de l'année 4045).

Lundi 12/09/22

Présents : D. Auroy, S. Faye, N. Genier et C. Le Conte

Bilan de la première séance de DPA réalisée en classe de 3e (voir le compte rendu à la date du lundi 05/09/22.

Discussions sur la progression annuelle donnée à l'alternante Mme Genier. Cette progression pause, de l'avis de tous, quelques problèmes d'organisation mathématique du fait de l'étude des nombres entiers, ou des fractions décimales, alors que les élèves nouvellement entrés en 6e n'ont, a priori, rien rencontré d'autre que la "fraction partage", qui ne peut pas être reliée à la "fraction nombre", c'est à dire à la mesure d'une grandeur.

C'est pourquoi, après discussion, l'ensemble des professeurs présents se sont entendus pour étudier le PER sur les fractions, mis au point par le Groupe Didactique de l'Irem de Marseille, travaillant au collège Puget (13006), et réunissant près d'une dizaine d'enseignants de mathématiques de quatre ou cinq collèges de Marseille, présidé par M. Yves Matheron, professeur d'université et didacticien de l'enseignement des mathématiques.

Ce travail commencera lundi 19/09/22.

Lundi 05/09/2022

Présents : D. Auroy, S. Faye, N. Genier et C. Le Conte

Reprise après deux mois d'arrêt.

Projets de cette année :

• Comme à l'accoutumée, l'objectif de ce labo est d'y poser toutes les questions que nous nous posons en tant qu'enseignants sur les savoirs de notre discipline : leurs raisons d'être, les questions ou activités à poser aux élèves pour introduire de nouvelles notions, l'ordre dans lequel il est préférable de rencontrer les différents types de tâches et leurs techniques. Pour parler didactique, il y est question d'organisation mathématique et d'organisation didactique. Le menu du site contient un onglet intitulé "La TAD" qui explique rapidement ce qui se cache derrière ces deux types d'organisations.
• En lien avec cet objectif, nous avons décidé cette année de tester les Dispostifs Préventifs d'Aide (DPA), pour les niveaux 6e, 5e et 3e que nous avons. Ces tests sont menés dans le but de contribuer à la recherche en Sciences de l'Education et en Didactique de l'enseignement des mathématiques, dans le cadre de la thèse commencée par M. Auroy.

En quoi consistent les DPA ?

Historique rapide

Les DPA sont une émanation de la TAD dans le sens où, si l'organisation didactique permet d'observer et de mettre en place les différents moments de l'étude, il n'en reste pas moins que les enseignants font face à des élèves qui éprouvent souvent des difficultés scolaires : notions de mathématiques très vagues, bases très approximatives voire absentes, curriculum vécu incomplets ou absents, etc. L'idée est donc venue de tester les élèves sur les prérequis dont l'absence pourrait nuire aux nouveaux apprentissages.

Organisation d'un DPA

Les travaux réalisés en primaire par le projet DIAS du groupe ADEF, appartenant à l'Université d'Aix-Marseille, conjointement avec une équipe de l'université de Scherbrook au Canada, ont permis d'organiser les DPA en quatre étapes :

1ère étape : un test sur la présence et la fiabilité des prérequis qui seront nécessaires aux nouveaux apprentissages.

2ème étape : un DPA "anté" qui a lieu avant le cours. Dans ce DPA "anté", les élèves pour lesquels le test a montré des lacunes sont "isolés" des autres pendant une période plus ou moins longue (de 20min à 50min) afin de travailler sur ces prérequis. Dans un DPA "anté", le temps didactique ne doit pas avancer : les élèves concernés par ce DPA ne prennent pas d'avance sur leurs camarades à propos des nouveaux apprentissages à venir. Ils se contentent de travailler, en groupe, sur les prérequis, avec un guidage du professeur qui doit s'efforcer de s'effacer le plus possible.

3ème étape : le cours proprement dit a lieu et des nouveaux apprentissages sont étudiés.

4ème étape : un DPA "post" est organisé afin de s'assurer que les élèves concernés par le DPA "anté" ont suivi le cours comme les autres et n'ont pas été "laissés sur le bord de la route".

Premier DPA de l'année 2022-2023 : l'arithmétique en classe de 3e

Lundi 05/09/22

Décision est prise de lancer un premier test en classe de 3e. Le thème de l'arithmétique est celui du premier chapitre qui doit débuter mercredi 07/09/22. Les types de tâches correspondants aux prérequis estimés nécessaire à la compréhension de son contenu ont été les suivants :

Lundi 05/09/22 après midi, le test a été créé.

Mardi 06/09/22

Passage du test dans deux classes de 3e.

Le mardi midi, les corrections de ce test étaient déjà commencées. Elles furent rapidement terminées afin que dès le lendemain la séance de DPA "anté" ait lieu avec, dans chaque classe, le groupe d'élèves n'ayant pas répondu correctement aux types de tâches \(T_1\) et \(T_2\) considérés comme indispensables pour bien débuter le chapitre à venir.

Mercredi 07/09/22

La correction des tests a établi, pour chaque classe, trois groupes d'élèves :

1. Un groupe d'environ \(7\) élèves possédant et sachant utiliser les termes attendus dans \(T_1\) et \(T_2\).
2. Un groupe d'environ \(16\) élèves ayant quelques souvenirs des termes attendus, mais leurs significations respectives étaient confuses et inadaptées aux reformulation attendus.
3. Un groupe n'ayant aucun souvenirs des termes attendus.

Il a été décidé de réunir les \(7\) élèves dans un groupe "fort", et les autres dans un groupe "faible" avec, pour ce dernier, les consignes suivantes :

Première séance de DPA "anté" assurée, pour une classe, en co-intervention, par Mme Faye et Mme Le Conte, la première prenant en charge le groupe "faible", la deuxième chargée de proposer des exercices variés sur le thème des multiples et diviseurs au reste de la classe (recherches des diviseurs d'un nombre donné, etc.). Pour l'autre classe, c'est Mme Faye seule qui a du gérer la même organisation que celle effectuée avec Mme Le Conte.

Ces deux séances se sont bien passées aux dires des professeurs concernées. Dans le groupe "faible", les discussions entre élèves ont permis de redonner du sens au vocabulaire pourtant rencontré déjà en 6e (cela a cependant été plus long avec la classe où Mme Faye a été seule pour tout gérer). Les résultats de ces discussions ont été validés à la fois par les élèves et par le professeur, à travers de nombreux exemples avec des "petits" nombres entiers. Une institutionnalisation de ce vocabulaire a eut lieu au cours suivant, juste avant le démarrage véritable du chapitre d'arithmétique.

Ce premier test n'a pas fait l'objet d'enregistrements vidéos ou audio par manque de temps en cette période de rentrée. Ce sera rectifié aux prochains.

---